4f atomic orbitals

For any atom, there are seven 4f orbitals. The f-orbitals are unusual in that there are two sets of orbitals in common use. The first set is known as the general set, this page. The second set is the cubic set, this page and these might be appropriate to use if the atom is in a cubic environment, for instance. Three of the orbitals are common to both sets. These are are the 4f_xyz, 4f_z³, and 4f_z(x²-y²) orbitals.

The higher f-orbitals ( 5f, 6f, and 7f) are more complex since they have one or more spherical nodes.

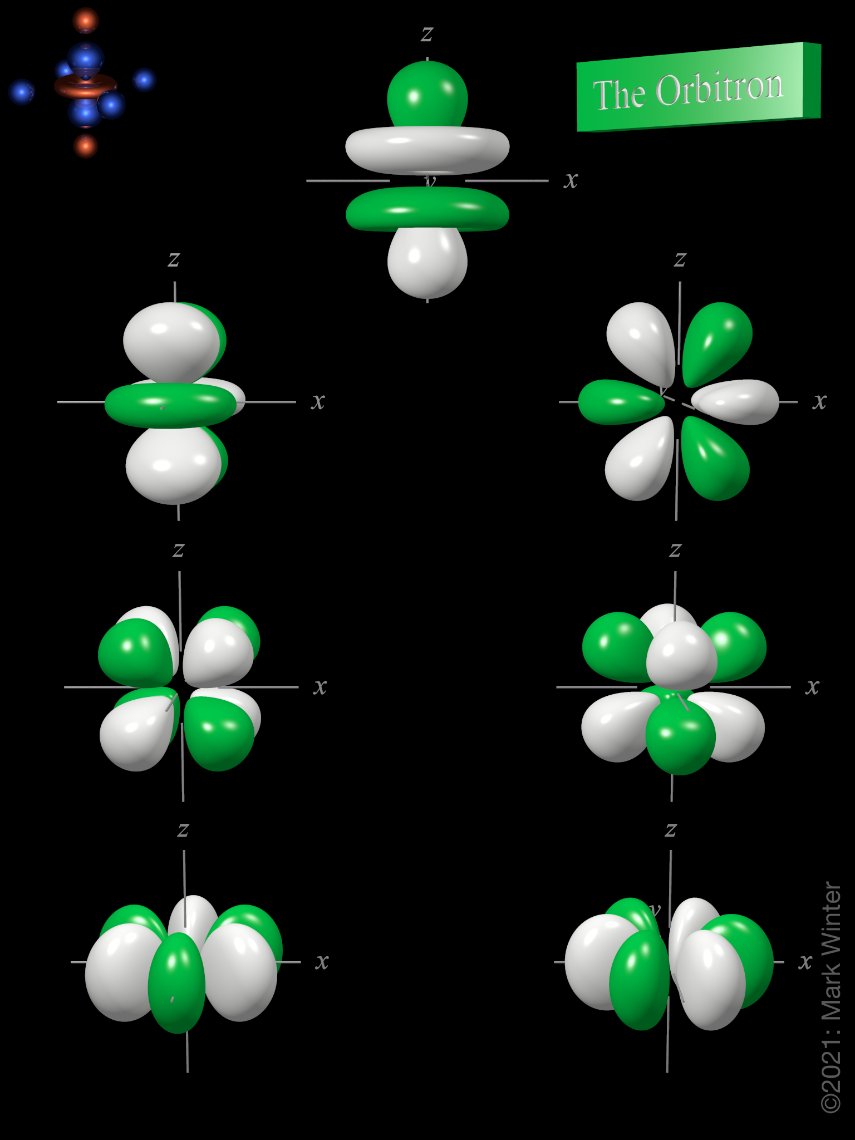
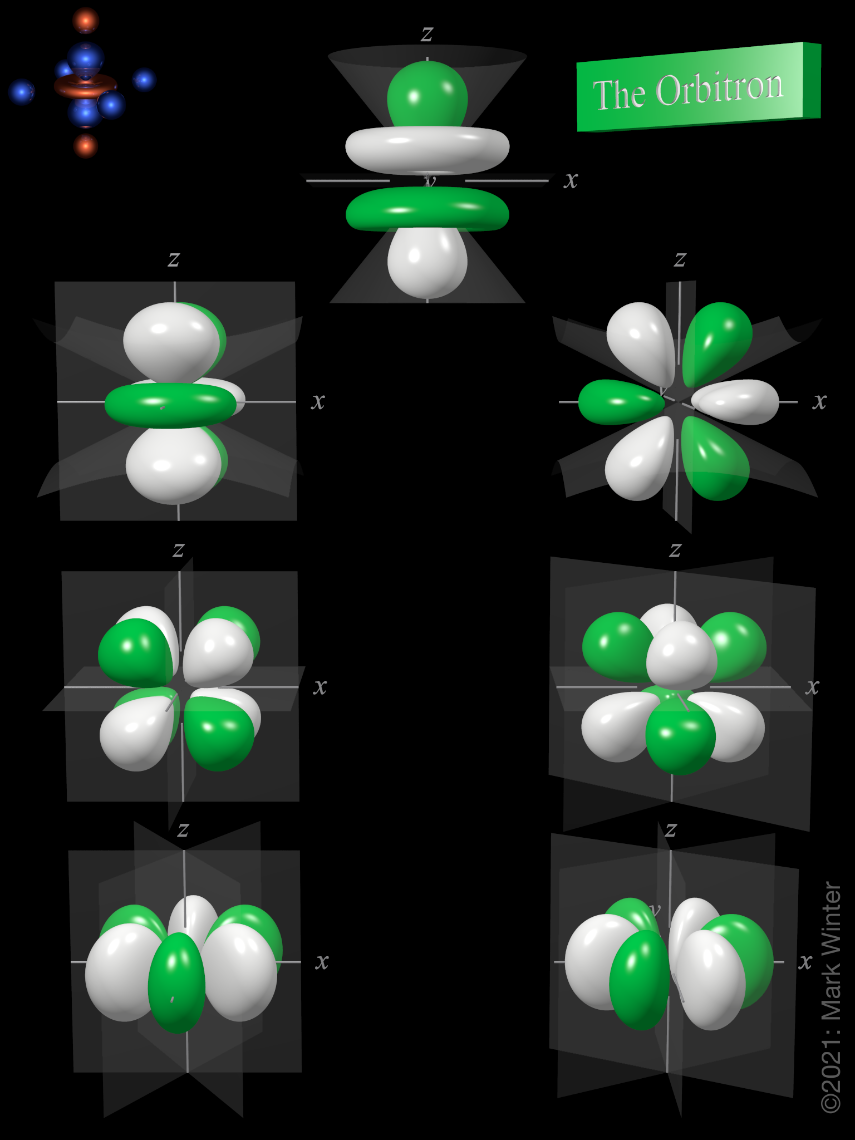
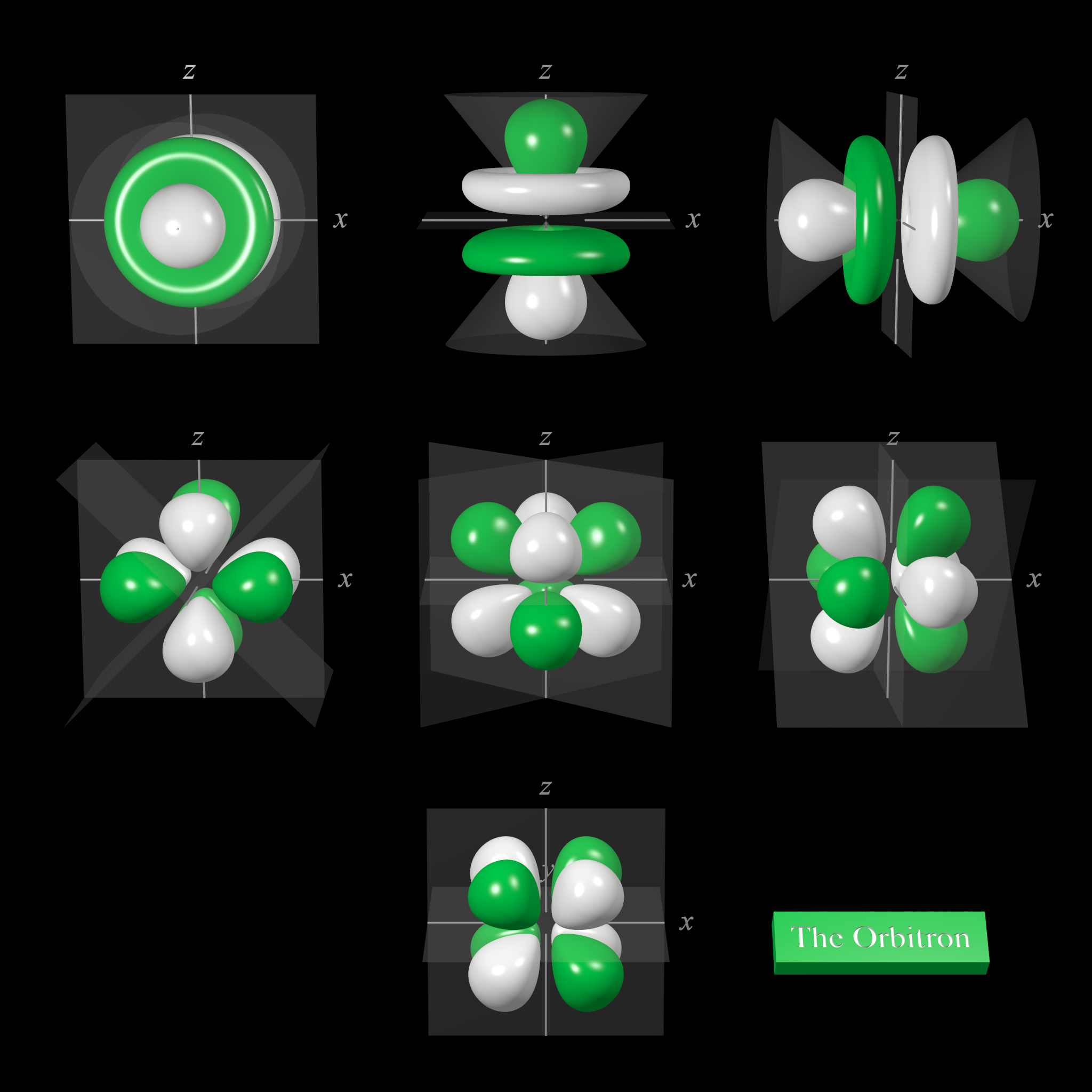
4f atomic orbitals general set

The shape of the seven 4f orbitals (general set). From left to right: (top row) 4f_z³, (next to top row) 4f_yz², 4f_xz², (next to bottom row) 4f_xyz, and 4f_z(x²-y²), (bottom row) 4f_y(3x²-y²), 4f_x(x²-3y²). For each, the green zones are where the wave functions have positive values and the white zones denote negative values.

The seven 4f orbitals. Use the previous and next icons to see other views

The seven 4f orbitals including orbital nodes. Use the previous and next icons to see other views

Nodes of the seven 4f orbitals. Use the previous and next icons to see other views

In the general set of 4f orbitals, there are four distinct shapes, each of which possess a number of planar and conical nodes. The 4f orbitals do not possess any radial nodes.

The 4f_z³ orbital (top row in the image above) has a planar node in the xy plane and two conical nodes with their exes along the z-axis.

The 4f_yz² and 4f_xz² orbitals (next to top row in the image above) are related to each other by a 90° rotation about the z-axis. At first sight, they are similar in shape to the 4f_y(3x²-y²) and 4f_x(x²-3y²) orbitals but they are not. While these orbitals contain six lobes, the nodal planes are not at 60° to each other and two of the six lobes are "bean-shaped".

The 4f_xyz and 4f_z(x²-y²) (next to bottom row in the image above) each have eight lobes and are related to each other by a 45° rotation about the z-axis. Each orbital has three nodal planes, which for the 4f_xyz are the xy, xz, and yz planes.

The 4f_y(3x²-y²) and 4f_x(x²-3y²) orbitals (bottom row in the image above) are related to each other by a 90° rotation about the z-axis. Each orbital has six lobes separated by three nodal planes lying at 60° to each other.

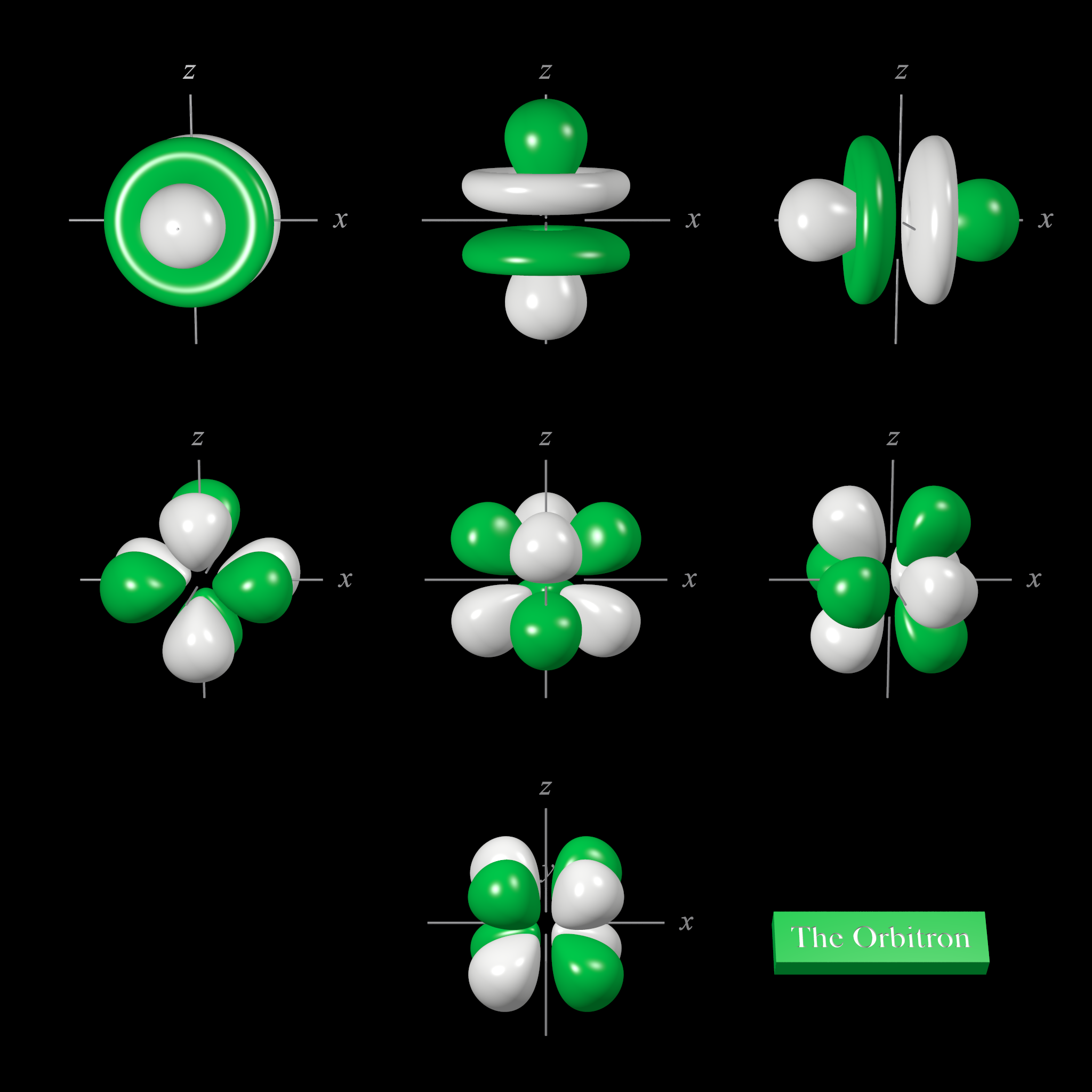
4f atomic orbitals cubic set

The shape of the seven 4f orbitals (cubic set). From left to right: (top row) 4f_y³, 4f_z³, 4f_x³, (middle row) 4f_y(z²-x²), 4f_z(x²-y²), and 4f_x(z²-y²) (bottom row) 4f_xyz. For each, the green zones are where the wave functions have positive values and the white zones denote negative values.

The seven 4f orbitals. Use the previous and next icons to see other views

The seven 4f orbitals including orbital nodes. Use the previous and next icons to see other views

Nodes of the seven 4f orbitals. Use the previous and next icons to see other views

In the cubic set of 4f orbitals, there are two distinct shapes, each of which possess a number of planar and conical nodes. None of the 4f orbitals possess radial nodes.

The 4f_xyz, 4f_x(z²-y²), 4f_y(z²-x²), and 4f_z(x²-y²) (bottom two rows in the image above) each have eight lobes. The 4f_x(z²-y²), 4f_y(z²-x²), and 4f_z(x²-y²) orbitals are related to each other by 45° rotations about the x, y, and z-axis respectively. Each orbital has three nodal planes, which for the 4f_xyz are the xy, xz, and yz planes.

The 4f_x³, 4f_y³, and 4f_z³ orbitals (top row in the image above) has a planar node in the xy plane and two conical nodes orientated along the z-axis. The other two orbitals are related through 90° rotations.