7d atomic orbitals

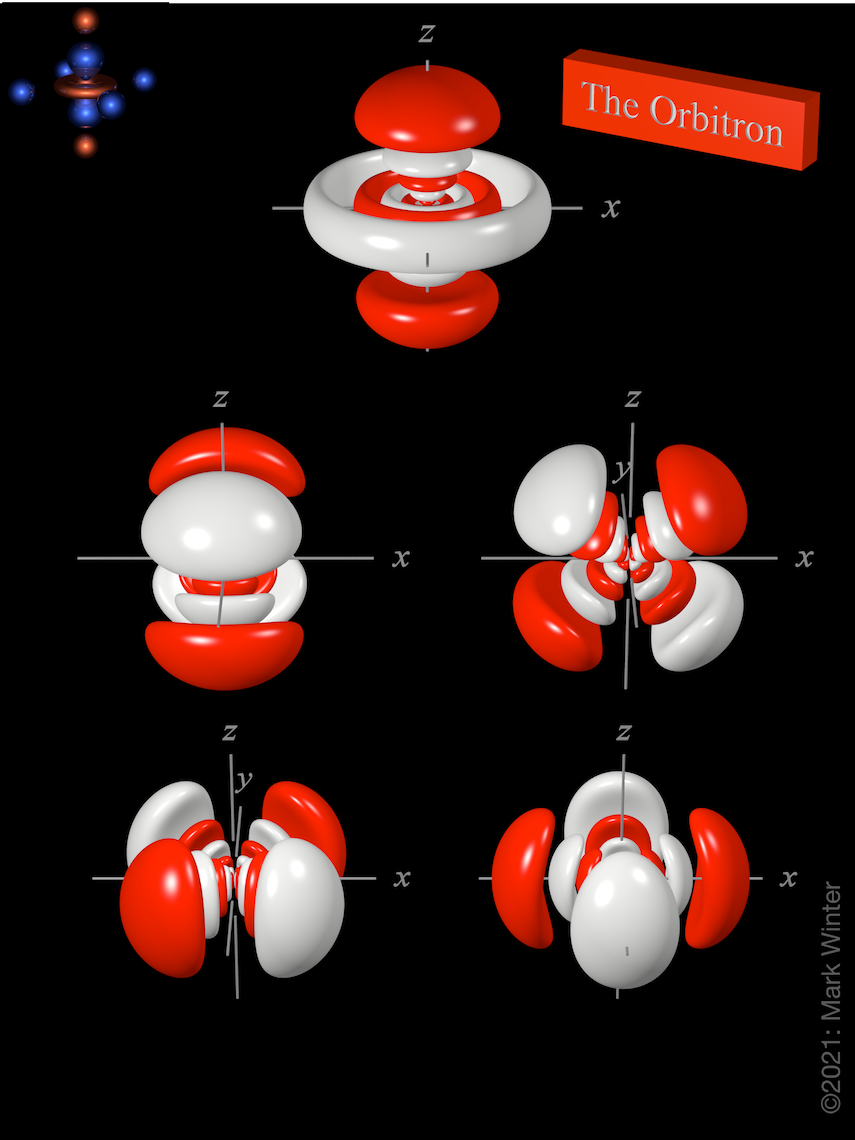
There are five 7d orbitals. These are labelled 7d_xy, 7d_xz, 7d_yz, 7d_x²-y² and 7d_z². The 7d_z² name is an abbreviation for 3d_(3z²–r²). Four of these functions have the same shape but are aligned differently in space. The fifth function (7d_z²) has a different shape.

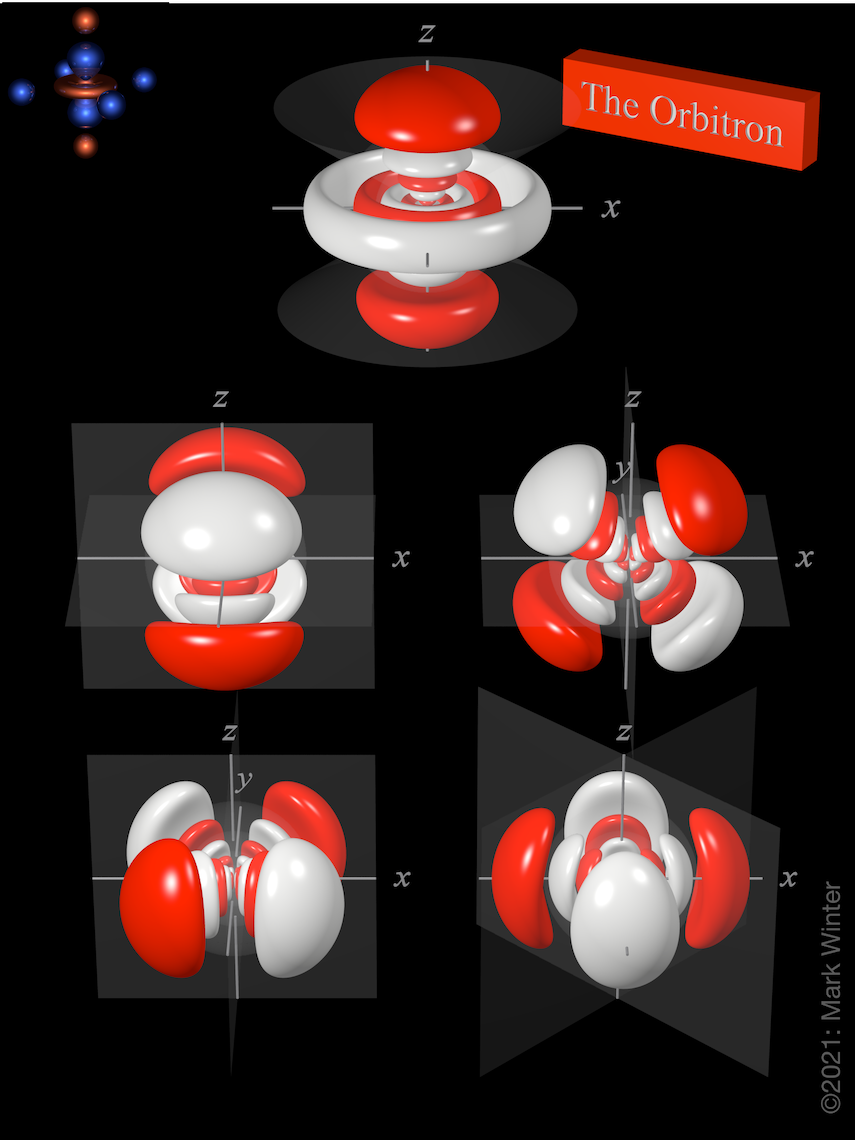
The shape of the five 7d orbitals. Top row: 7d_z²; centre row from left to right: 7d_yz and 7d_xz; bottom row: 7d_xy and 7d_x²-y². For each, the white zones are where the values of the wave functions are negative while the red zones denote positive values.

The five 7d orbitals. Use the previous and next icons to see other views

The five 7d orbitals including orbital nodes. Use the previous and next icons to see other views

Nodes of the five 7d orbitals. Use the previous and next icons to see other views

There are five 7d orbitals. These are labelled 7d_xy, 7d_xz, 7d_yz, 7d_x²-y² and 7d_z². Four of these functions have the same shape but are aligned differently in space. The fifth function (7d_z²) has a different shape.

Each 7d_xy, 7d_xz, 7d_yz, and 7d_x²-y² orbital has eight lobes. There are two planar node normal to the axis of the orbital (so the 7d_xy orbital has yz and xz nodal planes, for instance). The 7d_z² orbital is a little different and has two conical nodes. In addition, apart from the planar nodes, all five orbitals have three spherical nodes that partition off the small inner lobes. The lower d-orbitals ( 3d, 4d, 5d, and 6d) have fewer.

The origin of the planar nodes becomes clear if we examine the wave equation which, for instance, includes an xy term in the case of the 7d_xy orbital. When either x = 0 or y = 0, then there must be a node and this, by definition, is the case for the yz and xz planes.