 |
|---|
| VSEPR home |
|
|
| The University of Sheffield | |
| Department of Chemistry | VSEPR |
Isomers
The case of ClF3 is interesting. The calculation shows that the shape is based upon five electron pairs and the favoured geometry is therefore trigonal bipyramidal. There are three bonded groups and so two lone pairs. This is indeed the case, but the point of interest here is the location of the lone pairs. There are three possible ways of placing two electron pairs in a trigonal bipyramidal geometry.
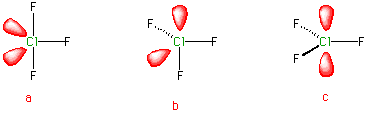
These three structures have respectively zero, one, and two lone pairs in the axial sites. For the VSEPR method to be worth much, it has to successfully predict the correct geometry. To approach this problem it is necessary to know the relative magnitude of the various kinds of electron pair-electron pair interactions. There are three possible interactions.
lone-pair ↔ lone-pair (lp ↔ lp)
lone-pair ↔ bond-pair (lp ↔ bp)
bond-pair ↔ bond-pair (bp ↔ bp)
Recall that lone pairs occupy more angular space and are located closer to their atoms than bond pairs. Given this, one can argue that the interactions between two lone pairs at any given angle are greater than the interactions between two bonding pairs. The interaction between a lone pair and a bonding pair is somewhere in between. Any given structure will adopt a configuration in which interactions between electron pairs are minimized. So, to make a comparison between the three plausible geometries for ClF3, it is necessary to compare the repulsions between the electron pairs in each of the three cases. A trigonal bipyramid has six interactions at 90°, three at 120° and one at 180°. The interactions for isomers a, b, and c are listed in Table 4.2.
| Structure | 90° | 120° | 180° |
|---|---|---|---|
| a | 2 bp ↔ bp 4 bp ↔ lp |
1 lp ↔ lp 2 lp ↔ bp |
1 bp ↔ bp |
| b | 2 bp ↔ bp 3 lp ↔ bp 1 lp ↔ lp |
1 bp ↔ bp 2 lp ↔ bp |
1 lp ↔ bp |
| c | 6 lp ↔ bp | 3 bp ↔ bp | 1 lp ↔ lp |
To a first approximation, one can disregard all the interactions that are greater than 90°. The effective distance between electron pairs for 120° and 180° angles is sufficiently large that their mutual interactions are small relative to the 90° interactions. This means that there are only the six interactions to address. Inspect the list of interactions in the 90° column and note that there is a common factor of three lp ↔ bp interactions for each. These three interactions can be 'cancelled out', leaving comparison of just three interactions (Table 4.3). Consider structures a and b. Relate two bp ↔ bp + one bp ↔ lp interactions for a with two bp ↔ bp + one lp ↔ lp interactions for b. The two bp ↔ bp interactions 'cancel' to leave a comparison of one lp ↔ bp with one lp ↔ lp interaction. The lp ↔ lp interaction is less stable and it is therefore concluded that a is more stable than b.
| Structure | 90° |
|---|---|
| a | 2 bp ↔ bp 1 bp ↔ lp |
| b | 2 bp ↔ bp 1 lp ↔ lp |
| c | 3 lp ↔ bp |
Now consider structures a and c. This involves comparing one lp ↔ bp + two bp ↔ bp interactions with three 3 lp ↔ bp interactions. One lp ↔ bp interaction is 'cancelled' out for each leaving a comparison of two bp ↔ bp with two lp ↔ bp interactions. Since bp ↔ bp interactions are less unfavourable than lp ↔ bp interactions, structure a is more favourable than c.
Since a is more favoured than either b or c, structure a is the most favoured structure. The geometry of ClF3 is therefore based upon a trigonal bipyramidal arrangement of five electron pairs but the 'visible shape' is 'T-shaped', as is indeed the case. Both electron pairs are equatorial.
Since the lone pairs occupy a little more than their fair share of the available space, the effect is for the three Cl-F bonds to squeeze together slightly to make room for the lone pairs. The trigonal bipyramid is therefore slightly distorted with the Claxial-F-Clequatorial bond angle less (87.5°) than 90°.
 |
|---|
|
|